素数の音楽

 面白い。この本は素数にまつわる歴史、その中でも数学の未解決問題のひとつである「リーマン予想」の証明に挑んだ数学者たちの物語だ。

次の素数がいつ現れるか、どうやったら素数を計算できるかと考えると、まったく規則性がないように見えるけれど、オイラーは見方を変えて、ある数までの間で、どのくらいの頻度、割合で素数が出て来るかと考えた。その素数の出現する割合がゼータ関数で近似できることをオイラーは発見する。

リーマンはそのゼータ関数を複素数全体に拡張すると、

ゼータ関数の自明でない零点はすべて実部1/2の直線上に存在する

と予想した。これがリーマン予想だ。ちなみにゼータ関数とはこんなの。

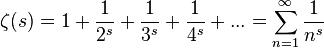
以上、自分でまとめてみたけれど、複素数については昔習ったことをおぼろげにしか覚えていないし、ゼータ関数については？？？だ。でも、この本は面白い。

ガウス、オイラー、セルバーグ、コンヌ、ラマヌジャン、エルデシュ、チューリングなどなど、素数の謎に挑んだ数学者達のお話が面白い。志村五郎という日本人の数学者も登場する。このひとは、ワイルズのフェルマーの最終定理を証明したときに重要な役割を果たした人らしい。アメリカのフライエレクトロニクスという電器屋の社長さんがリーマン予想の証明に向けて資金を出しているというのは初めて知った。フライはアメリカにいた頃はよくお世話になりました。数学という純粋な理論の世界に没頭できる数学者達の物語として読んでいるだけでも面白い。

もちろん、素数がインターネットのセキュリティーを支える基盤になっていることや、その仕組みも詳しく説明している。

数学自体は苦手だけれど、数学ものの本が好きな方におすすめです。是非一読を。

素数の音楽 (新潮文庫)